Women and Math, the Gender Gap Bridged

Yet five years into the 21st century, the leader of one of the world’s most elite universities, in one of the oldest democracies, opined upon “the unfortunate truth” that women probably are not as mentally equipped for work in math and science as men. So is it true?

A recent study in the journal Science shows that “the so-called gender gap in math seems to be linked to environmental factors, which means it could be eliminated by education or social programs.” So said Kellogg professor Paola Sapienza, one of the authors, along with Luigi Guiso (Instituto Universitario Europeo) and Ferdinando Monte and Luigi Zingales (both of the University of Chicago). In fact, Sapienza continued, “this gap doesn’t exist in countries in which there is greater gender equality.”

Better Grades, Poorer Scores

American girls, on average, earn higher grades than boys in most subjects in high school. According to the College Board, which administers the SAT college entrance exams in the United States, the average SAT-taking girl who graduated from high school in 2007 had a grade point average of 3.40, higher than the average boy’s 3.24. Girls were better represented than boys among the best students, comprising 57 percent of the SAT-takers who graduated among the top 10 percent of the class of 2007. Yet the girls’ average score on the math portion of the SAT was 499 points, compared with 533 for boys, out of a possible 800 (College Board 2007).

The math gender gap can be eliminated, and it is indeed eliminated in some countries. Since such math gender differences typically do not emerge until high school (Gallagher and Kaufman 2005), some argue that the tests themselves are biased (Spelke 2005). Others contend that, over time, social forces discourage talented women from studying science and math (Lubinski and Benbow 1992). “For example, the Study of Mathematically Precocious Youth shows that mathematically talented men were likely to go into engineering and the physical sciences, while similarly talented women tended more toward careers in law, medicine, and biology,” said Sapienza.

“With this evidence alone, it’s hard to tell whether girls’ and boys’ career choices are the result of social influence, or whether they reflect innate abilities,” continued Sapienza. “But there has been a trend—it’s very consistent with our story—showing that these differences in educational and professional choices are going away over time. So it must have something to do with the way society is evolving.” Sapienza went on to cite a 2006 study by Claudia Goldin, a Harvard economist, and colleagues on this topic.

Issues of Intrinsic Aptitude

Others dispute the role of social influences on male and female achievement, citing evidence that some basic mental attributes that are valuable for conducting math and science seem to be more developed among men. In a notable 1995 study, Larry Hedges and Amy Nowell analyzed data from six large studies to provide a comprehensive look at mental test scores for men and women. They concluded that “although average sex differences have been generally small and stable over time, the test scores of males consistently have larger variance.” Said Hedges, “The data show that there are simply more men than women who score at both the highest and lowest levels. This has important implications for achieving gender equity in society” (University of Chicago 1995).

This debate burst into public consciousness in 2005 when Harvard President and former Secretary of the Treasury Lawrence Summers, discussing why women are underrepresented in tenured positions at top science and engineering institutions, suggested that “in the special case of science and engineering, there are issues of intrinsic aptitude.” Although he added, “I would like nothing better than to be proved wrong,” the fuse had been lit.

Thus, we find ourselves again debating the roles of nature and nurture in human development. Are scientists the products of their inherited genetic gender code, or are they shaped by the gender-biased environments in which they live? Three months after Summers’ remarks, the Edge Foundation hosted a debate between psychology professors Steven Pinker and Elizabeth Spelke on the scientific evidence surrounding this issue.

Sapienza summarized the debate: “Pinker never claims that there’s no environmental factor. Spelke is more emphatic, claiming that there’s no shred of evidence for biology. As an economist, I believe both of them may have an impact, but I am more interested in understanding the relative importance of biology and culture.”

She continued, “If you tell me that 80 percent of the effect is biological, I know there’s limited opportunity for education policy to change things. But that’s not what we find. The math gender gap can be eliminated, and it is indeed eliminated in some countries.”

Turkey, Iceland, and PISA

In search of bridges across this gap, Sapienza and colleagues analyzed data from over 276,000 children in forty countries. The large number of subjects and the broad range of social systems represented were key to the validity of the study. “Devin Pope and Justin Sydnor had the same idea,” said Sapienza, referring to their 2007 study. “They’re looking at the gender gap in different states in the U.S. The study is somewhat limited, however, because there isn’t enough variability, for example, between Massachusetts and Texas, compared to the difference between Iceland and Turkey.”

Each child took the 2003 Programme for International Student Assessment (PISA) at the age of fifteen. Created by the Organisation for Economic Co-operation and Development, PISA is an internationally standardized assessment of math, reading, science, and problem-solving ability. Every participant got the same questions at the same age, and every question was approved by every participating country in order to eliminate cultural bias.

“PISA has been incredibly useful for helping countries understand how well students are prepared in various disciplines,” said Sapienza. “When results of the first PISA came out in 2001, German scores were surprisingly low, sparking intense national debate. Because U.S. students do particularly poorly in math, President Bush created a National Mathematics Advisory Panel.” This panel, created in 2006, recently released its recommendations, declaring math education in the U.S. “broken” and advocating mastery of the fundamental skills that underpin success in higher math (NMAP 2008, Glod 2008).

In their search for a math gender gap, Sapienza and colleagues did not have to look very hard. Despite the fact that girls spent 19.5 percent more time than boys on math homework, their average math scores were 2 percent lower (a difference of 10.5 points in scores). This finding persisted even when accounting for the fact that boys spent 2.3 percent more time in math classes. Not only did the average boy outperform the average girl, but a gap also existed between the best male and female students. Among those in the top 5 percent of test takers, there were only six girls for every ten boys.

While the overall global pattern shows that boys tended to outperform girls in math, the male advantage was not complete. In a few countries girls topped boys. For example, the average girl in Iceland scored close to 3 percent higher (14.5 points) than the average boy. And in Indonesia there were eleven girls for every ten boys in the top 5 percent of test takers. The flip-flop of the gender gap in those countries hinted to Sapienza and her colleagues that their methods might lead them to some interesting discoveries.

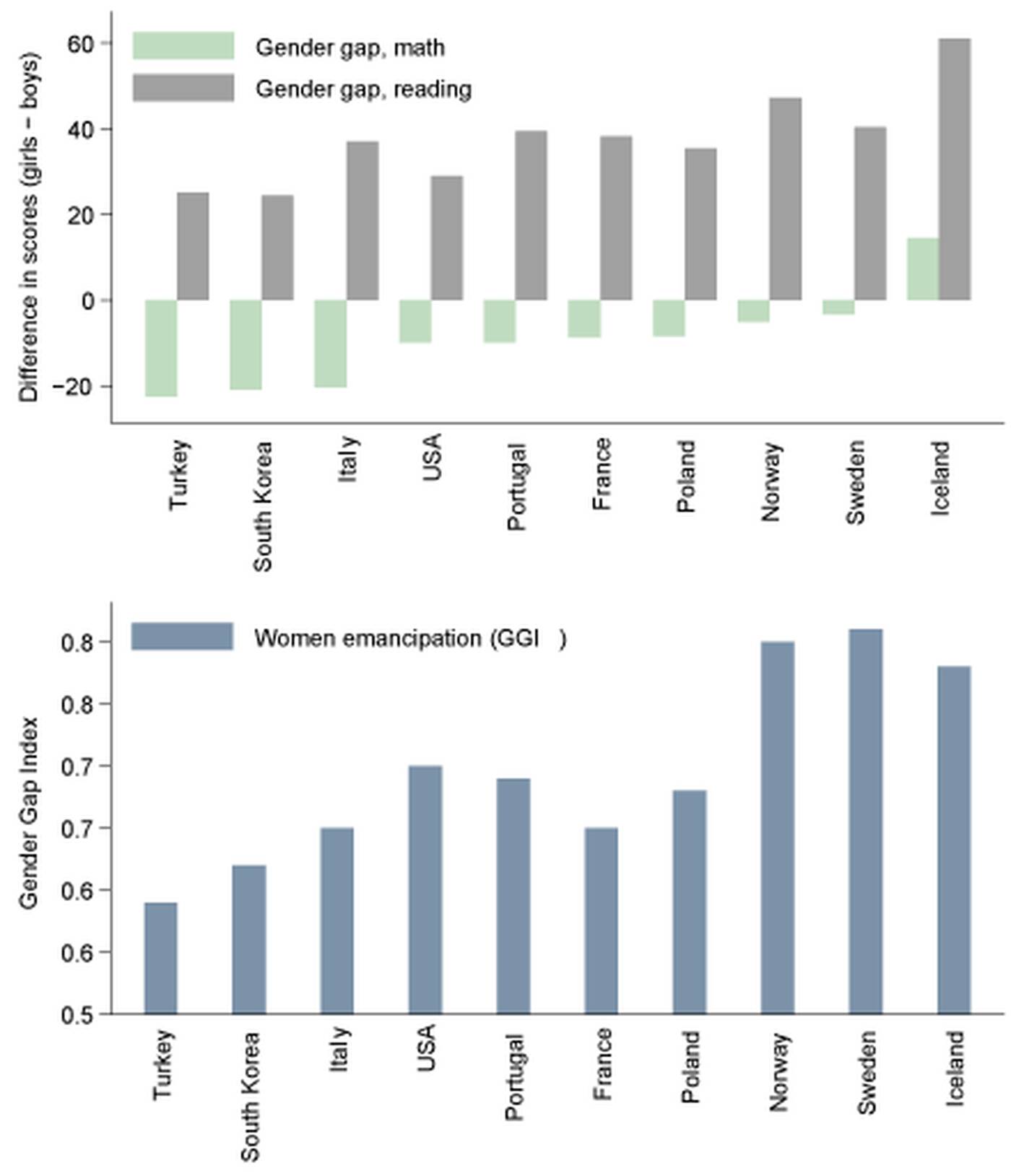
On measures of reading, the gender gap was turned on its head. There was not a single country in which boys outperformed girls. Worldwide average reading scores for girls were 6.6 percent better than for boys, ranging from 5.4 percent better in Turkey to 12.7 percent better in Iceland for the subset of countries shown in figure 1. Among children who scored in the top 95 percent, there were 183 girls for every 100 boys, ranging from a balanced one-to-one ratio among Turks to 29 girls for every 10 boys in Iceland.

“The shocking thing is how large the reading gap was. It’s almost more striking than the math gap findings, to see how the reading gap moves from country to country,” said Sapienza.

Moreover, the fluctuation in the reading gender gap across countries mirrors the fluctuation in the math gender gap. The two are statistically correlated (r = 0.59). Academic excellence is not specific to a single topic; countries that educate girls well do so across the board.

Empowered Women and Vanishing Gaps

Having recognized gender gaps that expanded and contracted from country to country, Sapienza and colleagues examined social features that might explain the changes. Other researchers had shown that social conditioning and gender-biased environments can impact test performance, so Sapienza and colleagues used four tools to measure how well women were integrated into each society compared with men. The first measure was the Gender Gap Index (GGI) developed by the World Economic Forum (WEF; see Hausmann et. al. 2006). “There are a number of variables that go into the Gender Gap Index,” said Sapienza. “For example, it measures resources given to women who want to work, such as maternity leave and child care facilities. Participation of women in labor is also a big factor, as is their role in political leadership.”

A second measure of gender equality was the World Values Survey, in which people around the world were asked how much they agreed or disagreed with statements such as “If a woman earns more money than her husband, it’s almost certain to cause problems” and “A university education is more important for a boy than for a girl.”

The researchers also analyzed the percentage of women aged fifteen or older who are available to work in each country’s labor force and the WEF political empowerment index, which measures the representation of women in government.

“We presented this, and many people from the U.S. didn’t like it. The majority of Americans are convinced that they’re at the top of the equality index. But they’re not. On some measures, the U.S. is below Estonia,” said Sapienza. The top four countries in the GGI ranking were Sweden (0.81), Norway (0.80), Finland (0.80), and Iceland (0.78). The U.S. is ranked 23rd (0.70). A GGI equal to 1 reflects full gender equality, a level none of the countries reached. “As a European, I’m not surprised that the top countries are the northern European,” said Sapienza, who hails from Italy, “but many people are surprised.”

Regardless of which measure of gender equality they used, Sapienza and her colleagues found that improved social conditions for women were related to improved math performance by girls. For example, the math gender gap almost disappeared in Sweden (GGI = 0.81), while girls scored nearly 23 points below boys in math in Turkey (GGI = 0.59). Not only did average girls’ scores improve as equality improved, but the number of girls reaching the highest levels of performance also increased. In Iceland, for example, there were 117 girls for every 100 boys among the top 1 percent of math students.

“We establish that in some countries the gender gap in math disappears. But there’s a big tension. Is it emancipation of women, or is it something else?” said Sapienza. “One possible explanation is wealth.”

To learn whether the math gender gap shrank as a result of girls in richer countries performing better than those in poorer countries, the researchers incorporated each country’s gross domestic product (GDP) into their mathematical model. Regardless of national differences in per capita GDP, the relationship between gender equality and the math gap remained. Improved roles for women in society, not simply economic development, predicted more gender-equal achievement in math. For example, Sapienza pointed out, “In some countries like Philippines or Sri Lanka, which aren’t particularly wealthy, women are fairly emancipated. On the contrary, some wealthy countries, like Italy, are among the less gender equal societies.”

Social Equality, or Just Biology at Work?

Having linked social structures to the math gender gap from country to country, Sapienza wonders whether this result rules out biological influences entirely. The answer is no. The biological hypothesis suggests that an average boy would score higher in mathematics than in reading, while for girls the reverse is true. This pattern does not change in more gender equal societies hinting that some aspects of academic performance may be innately different between boys and girls.

Sapienza and colleagues found that boys, regardless of the country and social environment in which they live, typically do better in math than in reading. Similarly, girls are usually better in reading than in math, regardless of the degree of gender equality in their society. As a result, in more gender equal societies, girls will gain an absolute advantage relative to boys.

Some evidence of the influence of biology can be gained by looking at mathematics sub-scores. Previous research had shown that boys’ advantage over girls in math is most pronounced in geometry (e.g., Pythagorean theorem), while the gap is narrowest in arithmetic (e.g., 1+2=3). But no matter how much girls narrow the gender gaps in geometry and arithmetic in more gender-equal countries, boys always score higher in geometry than arithmetic, while the opposite is observed for girls. So the between gender differences in a single discipline—reading or math—certainly appear to be influenced by social features, but the within gender differences between reading and math, and between arithmetic and geometry, appear to be much more stable across environments, suggesting possible biological roots.

Mechanism and consequences

Though these findings are fascinating and extremely important, they raise as many questions as they answer. It is not yet clear how important education is compared with other social features. “The big, important question is, ‘What’s the mechanism?’ ” said Sapienza. “What are these northern European countries doing so that there is no gap? Is it happening through role modeling? The kinds of jobs women get? Is it more acceptable for a woman to be a physicist in Sweden than in other countries? We simply do not know.”

In the United States, the number of female physicists and other scientists is increasing. The National Science Foundation reports that in 2006, 30 percent of full-time science and engineering faculty in the United States were women, up from 7 percent in 1973. In 2005, 39 percent of all U.S. science and engineering doctorates were earned by women, up from 27 percent in 1985 (NSF 2008). But while opportunities for women in science have greatly improved over recent decades, the words of Madame Curie written a century ago still resonate: “One never notices what has been done; one can only see what remains to be done.”

Moreover, the consequences of girls gaining an absolute advantage over boys are very interesting. “In many of the countries that we identified as more gender-equal, the percentage of women going to college outnumbers the percentage of men going to college,” said Sapienza.

“Given that boys spend much less time on homework and girls are catching up with the scores, are we going to see affirmative action for boys in colleges?” said Sapienza. “Some colleges, even in the U.S., are discussing these issues. If scores for girls go up and reach the level of Iceland or Sweden and you don’t decrease the threshold for admitting boys to college relative to girls, you’ll reach a situation with unbalanced admissions.”

While full global gender equity and academic achievement equality will not soon be reached, this work highlights successes and hints at some useful models. It may even offer glimpses of better times to come, a prospect that captures Sapienza’s imagination. She asked, “How do we think about these results? Has Iceland reached a level of total emancipation? Will it be the steady state, an equilibrium?”

She wondered, “Is this how societies are going to be in the future?”

Further readings:

Census Bureau (2006). “Facts for Features. Women’s History Month: March 2006.” Census Bureau Web site, February 22 (visit site, accessed May 28, 2008).

College Board (2007). 2007 College-Bound Seniors. Total Group Profile Report. College Board Web site (visit site, accessed May 28, 2008).

Edge Foundation (2005). The Science of Gender and Science. Pinker vs. Spelke: A Debate. Edge Web site (visit site, accessed May 28, 2008).

Gallagher, Ann M., and James C. Kaufman (2005). Gender Differences in Mathematics: An Integrative Psychological Approach. New York: Cambridge University Press.

Glod, Maria (2008). “Panel Urges Schools to Emphasize Core Math Skills.” Washington Post, March 14, page A6.

Goldin, Claudia, Lawrence Katz and Ilyana Kuziemko (2006). “The Homecoming of American College Women: The Reversal of the College Gender Gap,” Journal of Economic Perspectives, Fall, 20(4): 133-156.

Hausmann, Ricardo, Laura D. Tyson and Saadia Zahidi (2006). The Global Gender Gap Report 2006. Geneva: World Economic Forum (visit site, accessed May 28, 2008).

Hedges, L., and A. Nowell (1995) Sex Differences in Mental Test Scores, Variability, and Numbers of High-Scoring Individuals. Science, 269(5220): 41 – 45.

Lubinski, D., and C. Benbow (1992). “Gender Differences in Abilities and Preferences Among the Gifted: Implications for the Math/Science Pipeline”, Current Directions in Psychological Science, 1: 61-66.

Pope, Devin, and Justin Sydnor (2007). Nature, Nurture, and Sex Differences in Test Scores. Working paper, University of Pennsylvania.

National Science Board (2008). Science and Engineering Indicators 2008. National Science Foundation (NSF) (visit site, accessed May 28, 2008).

National Mathematics Advisory Panel (2008). Foundations for Success: Report of the National Mathematics Advisory Panel, U.S. Department of Education Web site (visit site, accessed May 28, 2008).

Spelke, Elizabeth (2005). “Sex Differences in Intrinsic Aptitude for Mathematics and Science?” American Psychologist, December, 60(9): 950-958.

Summers, Lawrence H. (2005). “Remarks at NBER Conference on Diversifying the Science & Engineering Workforce.” Harvard University Web site, Office of the President, January 14 (visit site, accessed May 28, 2008).

University of Chicago (1995). “New Study on Sex Difference in Mental Test Scores.” University of Chicago News Office, July 5, 1995 (visit site, accessed May 28, 2008).